Toute surface peut s’exprimer par la seule lettre \(S\).

Grâce à l’élément neutre de la multiplication, on peut écrire que \(S=1.S\), ce qui se lit par exemple “\(S\) est égale à une fois \(S\)”.

En écrivant \(S=1.S\), on dissocie la quantité de l’unité.

Par exemple, si l’on considère une surface de trois kilomètres carrés, on peut envisager cette surface globalement c’est-à-dire “trois kilomètres carrés” en une seule expression groupée par le biais de l’association des éléments ; on peut aussi dissocier la quantité “trois” de l’unité “kilomètre carré” par le biais de la multiplication car il s’agit bien de la quantité numérique “trois” multipliée par l’unité surfacique “kilomètre carré”.

Ainsi en écrivant \(1.S\), \(S\) est susceptible de devenir une quantité c’est-à-dire un nombre réel, et \(1\) l’unité. Cette unité est une surface : \(1.S\) signifie \(S\) fois une surface unitaire ayant pour valeur \(1\). Le plus simple est alors de considérer qu’il s’agit de la surface d’un carré d’où l’idée de quadriller le plan par des carrés ayant pour surface l’unité : c’est là une interprétation plausible de la nouvelle écriture \(1.S\) en remplacement de \(S\) tout court.

Le carré est évidemment très pratique non seulement parce qu’on peut en aligner plusieurs pour remplir une surface mais aussi parce qu’on calcule facilement la longueur de son côté, ce qui offre un renseignement supplémentaire précieux. Si le carré a pour surface \(1\), son côté a pour longueur \(\sqrt{1}\) soit \(1\). C’est là un cas particulier où la surface a la même valeur numérique que le côté mais il faut noter que dans l’écriture \(1.S\), le nombre \(1\) est une surface, on pourrait tout aussi bien écrire \(1^2.S\) pour mettre en évidence qu’il s’agit de carrés de \(1\) par \(1\).

Si maintenant ce carré a pour surface \(\alpha\), la surface s’écrit alors \(\alpha.S\).

Si toutefois on donne la longueur du côté du carré et non plus la surface de ces carrés de quadrillage, il faudra alors calculer la surface du carré qui sera le carré de cette longueur. Ainsi si le côté du carré de référence est \(\alpha\), la surface devient \(\alpha^2.S\), et ce, parce que la surface du carré de quadrillage est \(\alpha^2\).

Maintenant on peut s’affranchir du quadrillage et associer la surface \(S\) à une longueur arbitraire non nulle

qui est censée représenter la longueur du côté du carré de référence de quadrillage, même si cela ne se voit pas en l’absence de quadrillage explicite.

Si cette longueur est l’unité, la surface reste égale à \(S\) puisque le carré de référence correspondant a pour surface \(1\) ; mais si cette longueur est \(\alpha\), la surface devient \(\alpha^2.S\).

Ces deux surfaces \(S\) et \(\alpha^2.S\) ont une caractéristique importante : elles sont semblables. Il s’agit de deux formes semblables plus ou moins grandes en fonction de la grandeur du carré de quadrillage.

Cette similitude s’exprime par le fait que toute longueur \(l\) de \(S\) devient \(\alpha.l\) dans \(\alpha^2.S\), ce qui fait que tout couple de longueurs non nulles \(a\) et \(b\) d’un côté, et \(a’\) et \(b’\) de l’autre, est tel que \(\frac{a}{b}=\frac{a’}{b’}\) puisque \(\frac{a}{b}=\frac{\alpha.a}{\alpha.b}\) selon la notation canonique de la similitude sur la base de rapports arbitraires.

Dans un triangle rectangle, il existe une ligne très particulière : c’est la hauteur menée à partir de l’angle droit projetée à angle droit sur l’hypoténuse.

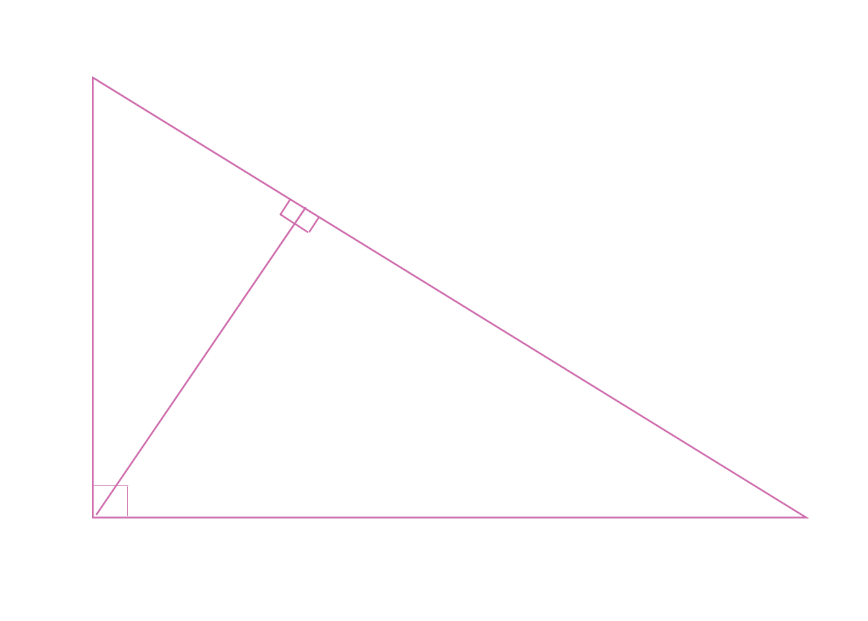
Elle a pour caractéristique de diviser le triangle rectangle en deux triangles rectangles non seulement semblables entre eux mais aussi semblables au triangle rectangle d’origine : les trois triangles rectangles sont semblables, ce qui explique la présence de trois carrés dans la formule de Pythagore, le carré étant l’expression de la similitude surfacique.

On a vu que toute surface pouvait être associée à une longueur arbitraire qui est la longueur des carrés d’un quadrillage du plan. On peut donc imaginer un quatrième triangle rectangle semblable qu’on associe à son hypoténuse unité. Appelons \(U\) la surface d’un tel triangle rectangle semblable puisque \(1.U=U\).

La surface d’un triangle rectangle semblable d’hypoténuse \(\alpha\) est alors \(\alpha^2.U\) : c’est le carré de l’hypoténuse multiplié par \(U\).

Ce qui donne immédiatement la formule de Pythagore car la surface du triangle rectangle semblable d’hypoténuse \(a\) est \(a^2.U\) ; la surface du triangle rectangle semblable d’hypoténuse \(b\) est \(b^2.U\) ; et la surface du triangle rectangle semblable d’hypoténuse \(c\) est \(c^2.U\).

On a bien \(a^2.U+b^2.U=c^2.U\) d’où en divisant la formule par \(U\)

\(a^2+b^2=c^2\)

Quod erat demonstrandum.